공학에서는 배열을 많이 사용하게 된다.따라서 배열을 계산하는 방법은 기본적으로 익혀야 한다.행렬의 덧셈과 뺄셈) – 행과 열의 크기가 각각 같은 배열에 대해서만 연산 가능 – 같은 위치의 원소를 각각 더하거나 뺀다

C행렬은 덧셈이므로 같은 위치의 원소를 더해 행렬로 나타낸 것이다.D행렬은 뺄셈이므로 같은 위치의 A원소-B원소를 한 결과를 행렬로 나타낸 것이다.
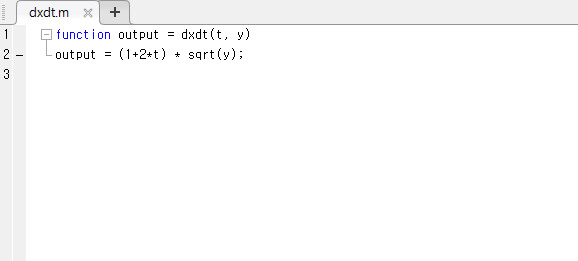
행렬에 스칼라 값을 덧셈 뺄셈 곱셈 나눗셈을 할 경우 계산하고자 하는 행렬의 모든 원소에 스칼라 연산을 각각 해준다.행렬 곱셈)-행렬 곱셈이 불가능한 경우를 주의하면서 계산하면 된다.행렬의 곱은 앞행렬의 열 수와 뒤에 계산되는 행렬의 수가 같아야 한다.A = (m, n) 행렬이면 B = (n, k) 행렬의 형태로 n값이 같아야 승산이 있다. m과 k의 값은 관계없다.- 행렬의 곱은 교환법칙이 성립하지 않으니 유의하자.
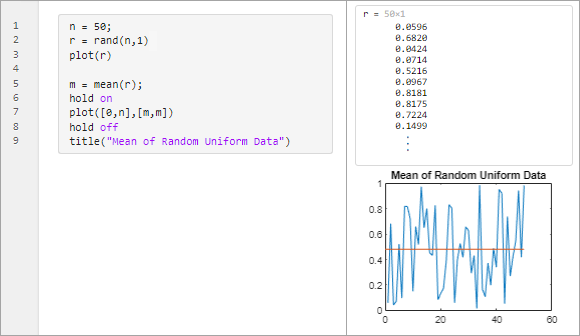
A(2.3)、B(3.2)
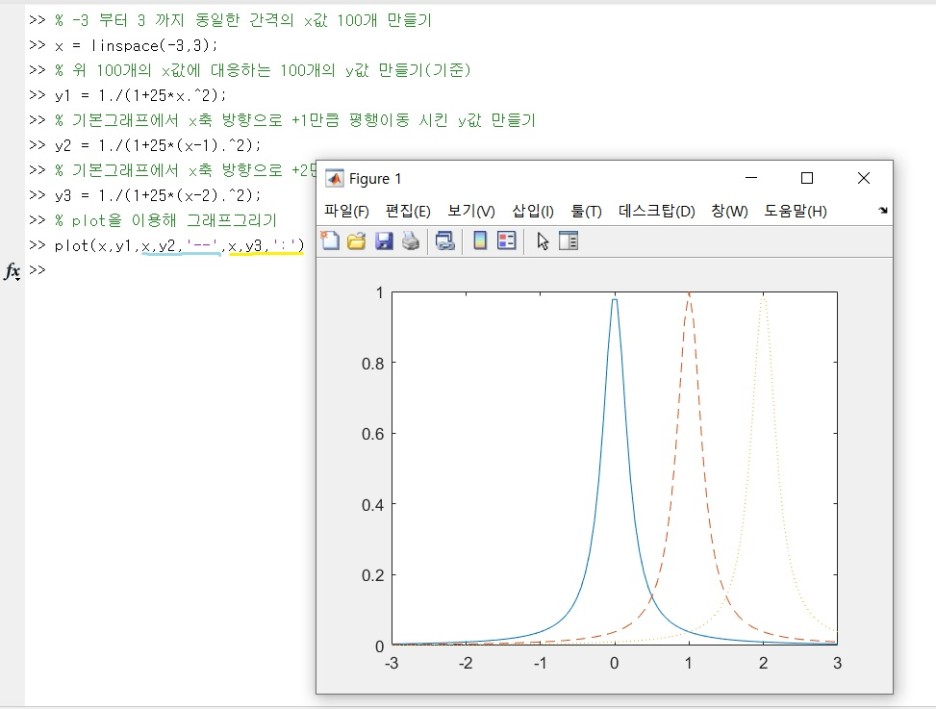
A * B = (2, 3) * (3,2) 그러므로 곱셈이 가능하고 결과는 2행 2열의 행렬을 이루었다.B * A = (3, 2) * (2,3) 그러므로 곱셈이 가능하고 결과는 3행 3열의 행렬을 이루었다.따라서 A*B와 B*A가 같지 않음을 알 수 있다.행렬의 나눗셈) 행렬의 나눗셈을 이해하기 위해서는 알아야 할 개념이 몇 가지 있다.- 항등행렬(단위행렬) 대각선 원소가 모두 1이고, 그 이외의 원소는 0인 정사각형 행렬 MATLAB에서는 eys(n) 명령어 사용 행렬에 단위행렬을 곱해도 값이 변하지 않는다.

A * eye(3) 값이 A행렬 값과 같다.

– 역행렬 A * B = B * A = I (단위행렬) 이 성립하는 A 와 B는 서로 역행렬 관계이다.MATLAB에서 A의 역행렬은 A^-1 또는 inv(A) 명령어를 사용한다.
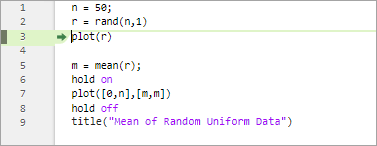
-0.00가 나온건 값이 작아서 0이라고 생각해

B 행렬을 A의 역행렬로 정의하고 역행렬인지 확인해 보았다.A * B = B* A의 결과가 동일함을 알 수 있다.- 행렬식 역행렬이 존재하기 위한 조건을 알아보기 위해 행렬식이 사용 행렬식 determinant = 0이면 역행렬이 존재하지 않는다.MATLAB에서는 det(A) 명령어를 사용한다.

-Ax=b의 해답x를 요구하는 2가지 방법-역행렬 이용 Ax=b→ inv(A)*Ax=inv(A)*bMATLAB명령:x=inv(A)*b-좌 나눗셈 이용 왼손 나눗셈을 이용하면 Gauss소거 법을 이용하고 계산하게 된다.MATLAB명령:x=A.b결과값이 동일함을 알 수 있다.이론적으로는 같지만 계산 방법이 서로 다르다.행렬의 크기가 크면 정확도 측면에서 가우스 소거법을 이용하는 좌나눗셈이 유리하다.원소별 연산) 두 행렬의 원소와 원소 간의 곱셈, 나눗셈, 덧셈 등을 연산할 수 있다. 점(.) 뒤에 연산 기호를 붙여 계산하면 된다.기호 설명 * 원소별 곱셈.^원소별 누승/원소별 우나눗셈.\원소별 좌나눗셈기호 설명 * 원소별 곱셈.^원소별 누승/원소별 우나눗셈.\원소별 좌나눗셈내장함수에서의 배열사용) 내장함수의 입력인자가 행렬인 경우-함수에 의해 정의된 연산이 원소별 연산과 같이 배열의 각 원소에 대해 이루어진다.- 출력은 입력 행렬과 같은 크기의 행렬이 된다.내장함수에서의 배열사용) 내장함수의 입력인자가 행렬인 경우-함수에 의해 정의된 연산이 원소별 연산과 같이 배열의 각 원소에 대해 이루어진다.- 출력은 입력 행렬과 같은 크기의 행렬이 된다.함수 설명 예 mean(A)A가 벡터, 행렬이라면 원소의 평균치를 일러 준다.>>A=[59 24];>>mean(A)ans=5C=max(A)A가 벡터인 경우 C는 A에서 가장 큰 원소이다.A이 행렬의 경우 C는 A의 각 줄에서 가장 큰 원소로 구성된 행 벡터이다.>>A=[1 2 3;456;7 8 9];>>C=max(A)C=7 8 9[d, n]=max(A)A가 벡터라면 d는 A에서 가장 큰 원소인, n은 원소의 위치이다.(최대치가 복수 있는 경우는 처음의 최대치의 위치).>>A=[59 2 4 11 6 11 1];>>[d, n]=max(A)d=11n=5min(A)최소치를 찾는다는 점을 제외하고 max(A)과 마찬가지>>A=[1 2 3;456;7 89];>>C=min(A)C=12 3[d, n]=min(A)최소치를 찾는다는 점을 제외하고[d, n]=max(A)과 마찬가지>>2;0>0>함수 설명>>A=[5924];>B=[2-2 1;3 2-1;2-32];>a=[12 3];>b=[24 1];sum(v)v:벡터 원소의 합>>sum(A)ans=20sort(v)v:벡터 원소를 오름차순으로 정렬>sort(A)ans=24 59median(v)v:벡터 원소의 중앙값(5,000median(v)v:벡터 원소의 중앙값>dianoss(a, b)a, b:벡터(원소 3개)두 벡터의 외적>>cross(a, b)ans=-53-2inv(B)B:정방 행렬 역행렬>>inv(A)ans=0.2000 0.2000-1.6000 1.0000-2.6000 0.4000 2.0000함수설명>>A = [5924]; > B = [2-2 1; 3 2-1; 2-32]; > a=[12 3]; > b=[241]; sum(v)v: 벡터 원소의 합> sum(A)ans = 20sort(v)v: 벡터 원소를 승순으로 정렬> sort(A)ans = 2459median(v)v: 벡터 원소의 중앙값 (5,000median(v) v:벡터 원소의 중앙값>dianoss(a, b)a, b:벡터 (원소 3개) 두 벡터의 외적 >> cross(a,b)ans = -53-2inv(B)B : 정사각행렬역행렬 >> inv(A)ans = 0.2000 0.2000 – 1.6000 1.00 – 2.6000 0.4000 2.00함수설명>>A = [5924]; > B = [2-2 1; 3 2-1; 2-32]; > a=[12 3]; > b=[241]; sum(v)v: 벡터 원소의 합> sum(A)ans = 20sort(v)v: 벡터 원소를 승순으로 정렬> sort(A)ans = 2459median(v)v: 벡터 원소의 중앙값 (5,000median(v) v:벡터 원소의 중앙값>dianoss(a, b)a, b:벡터 (원소 3개) 두 벡터의 외적 >> cross(a,b)ans = -53-2inv(B)B : 정사각행렬역행렬 >> inv(A)ans = 0.2000 0.2000 – 1.6000 1.00 – 2.6000 0.4000 2.00